|
 Термином «золотое сечение» пользуются художники, архитекторы, биологи, музыканты и даже поэты. Так что такое «золотое сечение» и почему его называют золотым? Чтобы понять это, проведем маленький опыт.
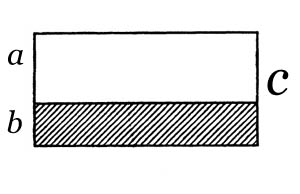
Представьте, что вы рисуете картину и вам необходимо провести на предназначенном для неё листе линию горизонта. Скорее всего, интуитивно, вы нарисуете её так, как показано на рисунке.
На этом рисунке отношение общей высоты картины к расстоянию от её верхнего края до нарисованной линии горизонта равно отношению расстояния от верхнего края картины до нарисованной линии горизонта к расстоянию от линии горизонта до нижнего края картины. То есть:
c:a = a:b
Это отношение или пропорция и называется «золотое сечение».
Эту существующую в природе пропорцию заметили ещё древние архитекторы и использовали её при строительстве, например, древнеегипетских пирамид. Позже она очень заинтересовала геометров Древней Греции, а художники всегда использовали её при рисовании картин. Великий Леонардо да Винчи заметил эту пропорцию в строении тела человека, он же и назвал её «золотым сечением».
Что такое золотое сечение мы разобрались, а чему оно равняется?
Чему равно золотое сечение
Если на приведенном рисунке высоту картины считать равной 1 (с = 1), а расстояние от верхнего края картины до горизонта обозначить, как X (a = X), то исходя из соотношения золотого сечения, мы получим уравнение:
1:X = X:(1 - X)
Преобразовав его, получаем уравнение:
X2 – X – 1 = 0
Положительный корень (решение) этого уравнения равен:
(√5 + 1) / 2 = 1,618…
Иногда эту величину обозначают греческой буквой τ (тау), иногда буквой φ (фи).
Золотое сечение в некоторых геометрических фигурах
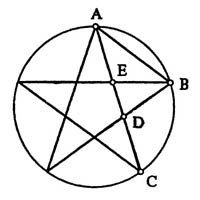
Самым наглядным образом золотое сечение представлено в изображении пятиконечной звезды (пентаграммы). Так точка D на рисунке делит отрезок CA в соотношении τ (золотого сечения), в этом же соотношении она делит и отрезок AE;
Длины отрезков AC и AB, так же, как и длины отрезков AB и AD, тоже находятся в соотношении золотого сечения.
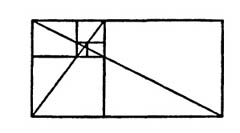
Ещё один интересный пример. Если от четырехугольника, стороны которого находятся в соотношении золотого сечения, отрезать квадрат, то останется прямоугольник, стороны которого также будут находиться в соотношении τ. Если от него снова отрезать квадрат, то стороны оставшегося прямоугольника опять будут пропорциональны друг другу в золотом соотношении и так далее.
|
